Introduction
The Outbreak
The 2014 Ebola outbreak in West Africa is an ongoing public health crisis, which has killed hundreds of people so far. The cross-border nature of this epidemic, which has emerged in Gunea, Liberia and Sierra Leone has complicated mitigation efforts, as has the poor health infrastructure in the region. While there has been much analysis and speculation about the factors at play in the spread of the virus, there aren't many specific predicitons about the expected duration and severity of this particular epidemic. In the (certainly temporary) absence of peer reivewed epidemic forecasts, this document explores a simple spatial SEIR model to make some initial forecasts.
The Data
A summary of the WHO case reports is very helpfully compiled on wikipedia for analysts who are too lazy to read the case reports themselves. Let's read it in with the xml library:
With data in hand, let's begin where every analysis should begin: graphs.
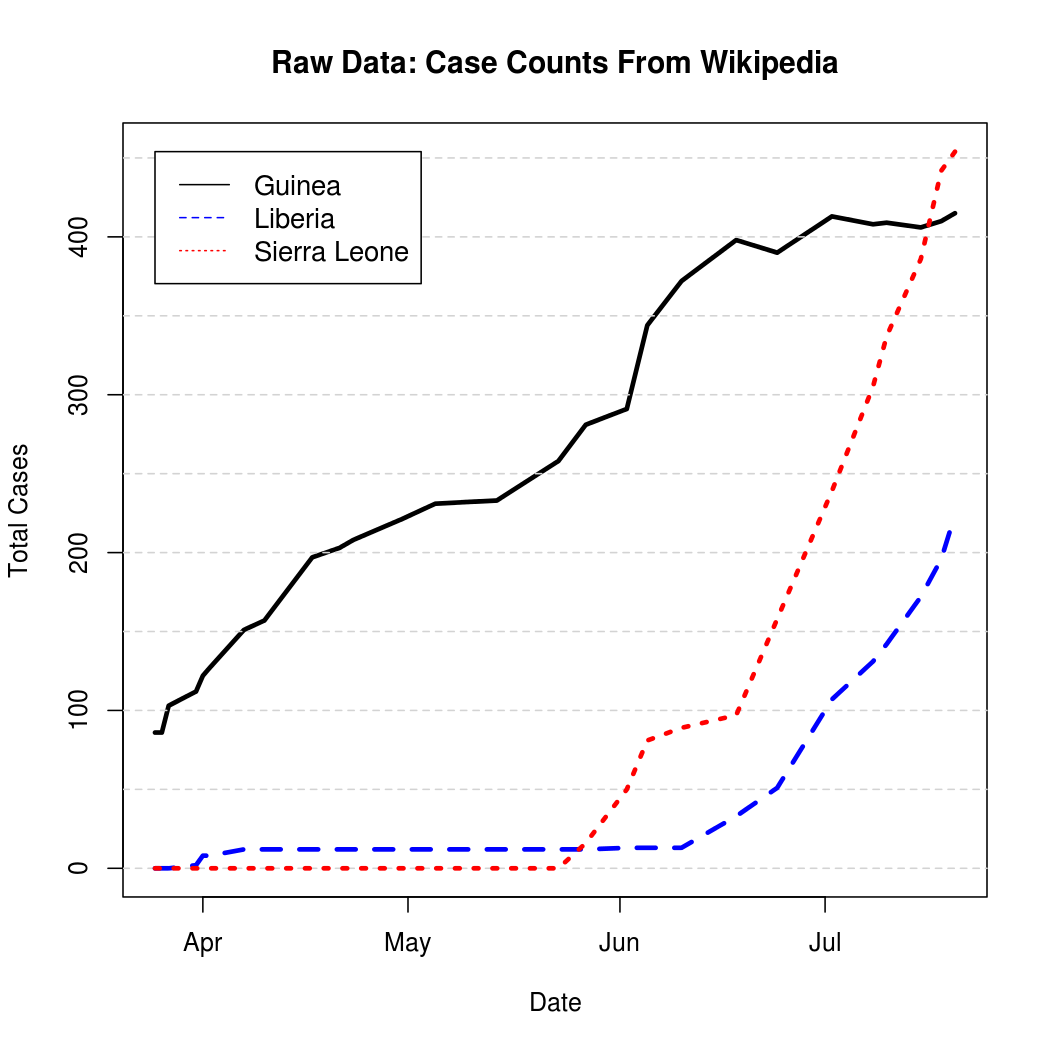
These represent cumulative counts, but because case reports can be revised downward due to non-Ebola illnesses the graphs are not monotone. If someone would hire an intern to read all the case reports and compile their best guess as to actual case infection times, that would be pretty awesome. Instead, let's just "un-cumulate"* the data and bound it at zero to get a rough estimate of new case counts over time.
*Unlike uncumulate, decumulate is actually a word. Unfortunately it just means "to decrease", and so was unsuitable for use here. There should probably be a word for uncumulating things, perhaps uncumulate.
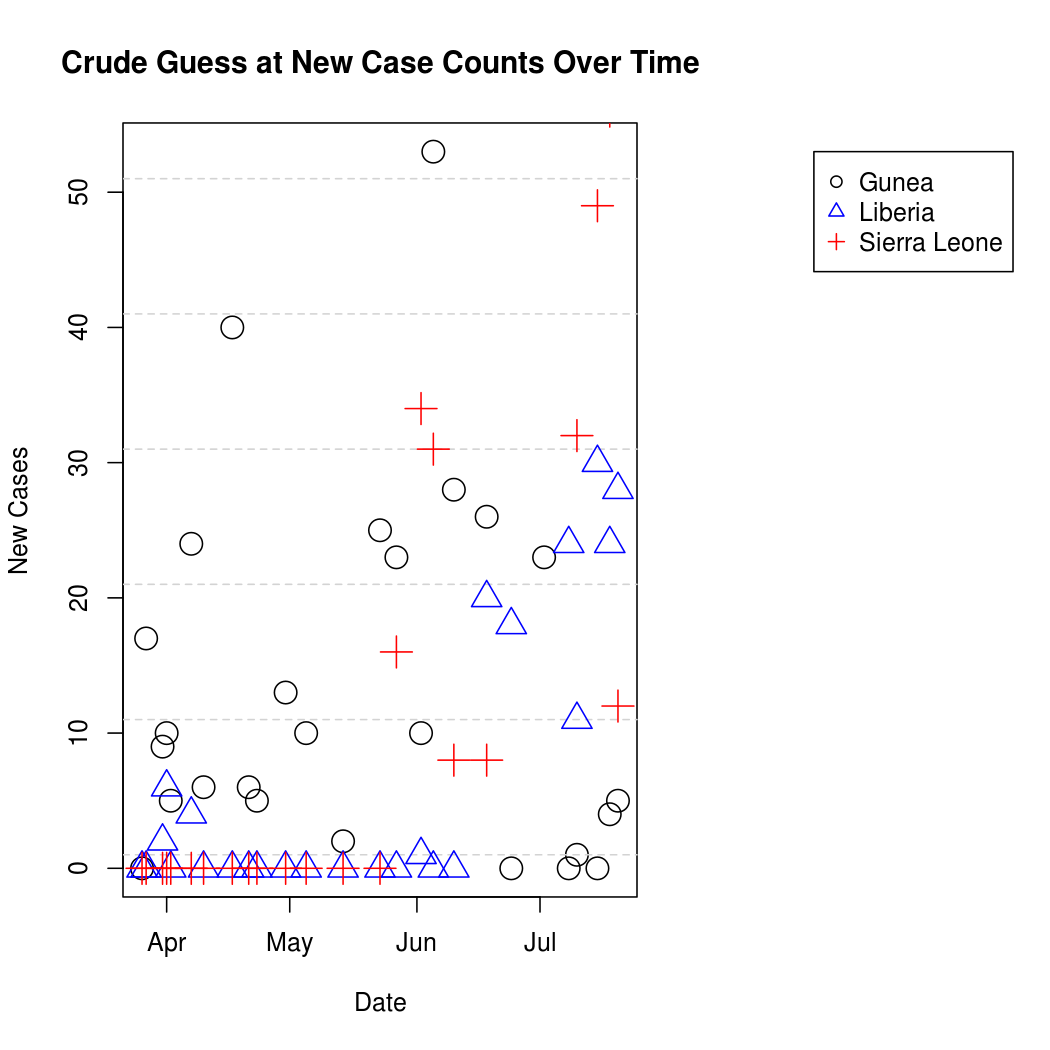
Here's a look at the "un-cumulated" counts. The process is a bit noisier from this perspective.
Compartmental Models
Now that we've got data read in and made a couple of plots to ensure we haven't done anything to terribly stupid with it
, let's do some compartmental epidemic modeling. Not only has Ebola been well modeled in the past using compartmental modeling techniques, but this author happens to be working on a software library designed to fit compartmental models in the spatial SEIRS family. What a strange coincidence! Specifically, we'll be using heirarchical Bayesian estimation methods to fit a spatial SEIR model to the data.
While a full treatment of this field of epidemic modeling is (far) beyond the scope of this writing, the basic idea is pretty intuitive. In order to come up with a simplified model of a disease process, discrete disease states (aka, compartments) are defined. The most common of these are S, E, I, and R which stand for:
- Susceptible to a particular disease
- Exposed and infected, but not yet infectious
- Infectious and capable of transmitting the disease
- Removed or recovered
This sequence traversed by members of a population (S to E to I to R) forms what we might call the temporal process model of our analysis. This analysis belongs to the stochastic branch of the compartmental modeling family, which has its roots in deterministic systems of ordinary and partial differential equations. In this framework, transitions between the compartments occur according to unknown probabilities. It is the S to E probability, which captures infection activity, into which we introduce spatial structure. Some details of this are given as comments to the code below, and more information than you probably want on the statistical particulars is available in this pdf document. For now, suffice it to say that we'll place a simple spatial structure on the epidemic process which simply allows disease to spread between the three nations involved, and we'll try to estimate the strength of that relationship. Many other potential structures are possible, limited primarily by the ammount of additional research and data compilation you are willing to do.
We're not going to do anything fancy with demographic information or public health intervention dates. Demographic parameters are relatively difficult to estimate here, as there are only three spatial units which are all from the same region. Intervention dates are more promising, but their inclusion requires much more background research than we have time for here. In the interest of simplicity and estimability, we'll just fit a different disease intensity parameter for each of the three countries in addition to as a set of basis functions to capture the temporal trend.
Analysis 1
Set Up
There are some things we need to define before we can start fitting models and making predictions.
- The time points are not evenly spaced, so we need to define appropriate offset values to capture the ammount of aggregation performed (time between reports).
- We must define the spatial correlation structure.
- A set of basis functions needs to be chosen to capture the temporal trend.
- Prior parameters and parameter staring values must be specified for each chain.
- A whole bunch of bookkeeping stuff for which I haven't yet programmed sensible default behavior needs to be set up.
More details are available in comments to the code below.
With the set up out of the way, we can finally build the models. In order to assess convergence, we'll make three model objects - one for each MCMC run.
With the model objects created, let's do some short runs for each chain to try to choose sensible Metropolis tuning parameters. The following script uses the runSimulation function defined in the previous code block to do just that.
Now we can run the three chains for longer in order to acheive convergence. As before, we'll adjust the tuning parameters along the way. Astute readers may notice the frankly inconvenient number of samples requested , and will correctly infer that autocorrelation is currently a major problem for this library. This problem is being worked on.
Convergence Diagnosis
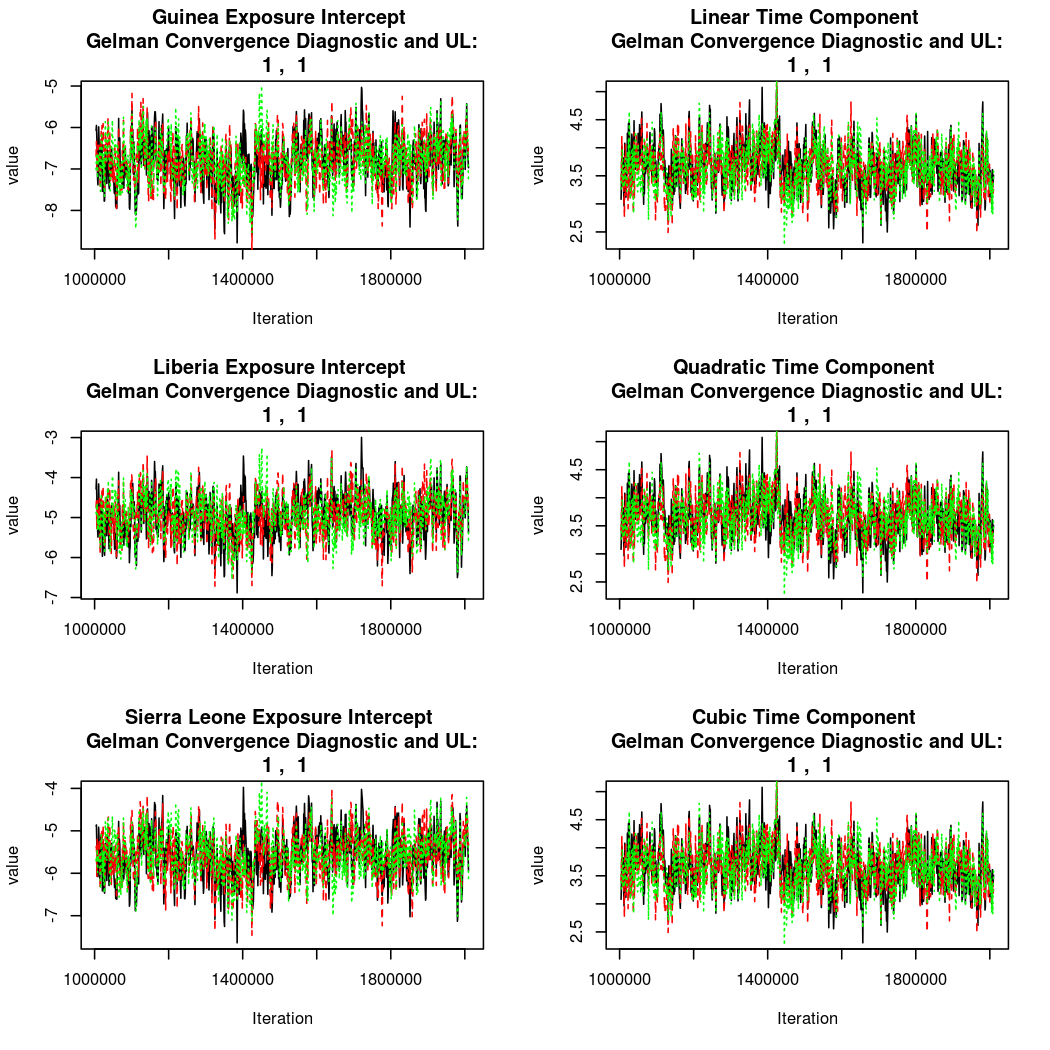
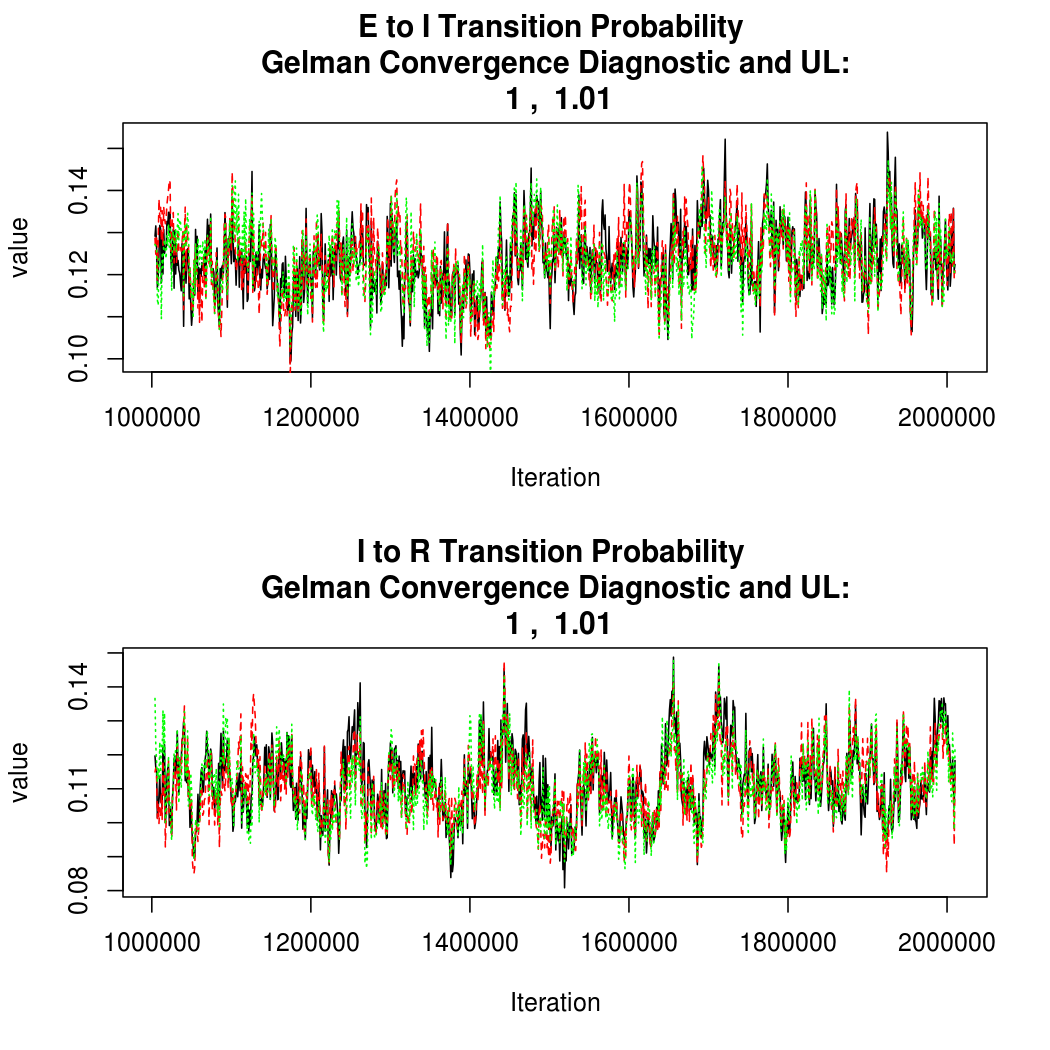
As this is a Bayesian analysis in which the posterior distribution is sampled using MCMC techniques, we really need some indication that the samplers have indeed converged to the posterior distribution in order to make any inferences about the problem at hand. In the code below, we'll read in the MCMC output files created so far, plot the three chains for each of several important parameters, and take a look at the Gelman and Rubin convergence diagnostic (which should be close to 1 if the chains have converged.)
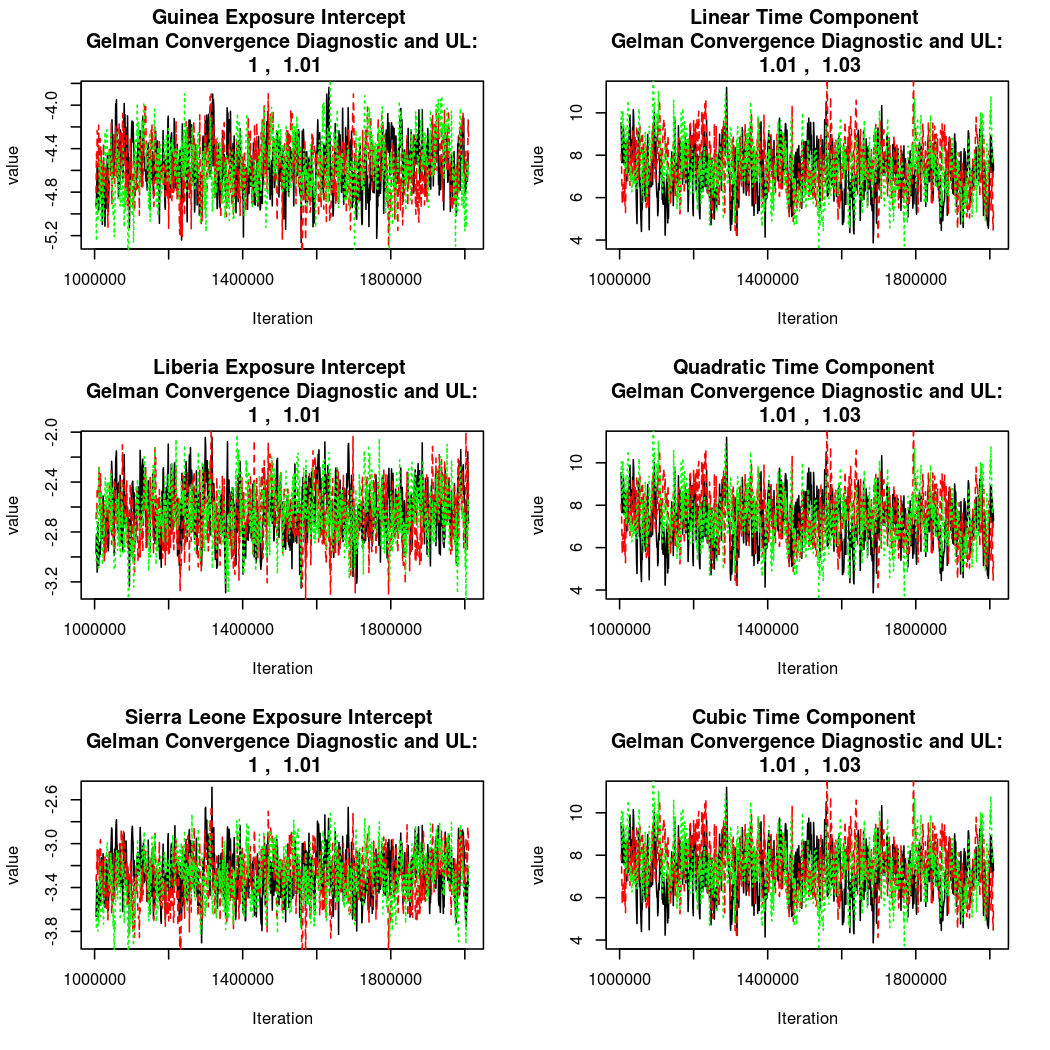
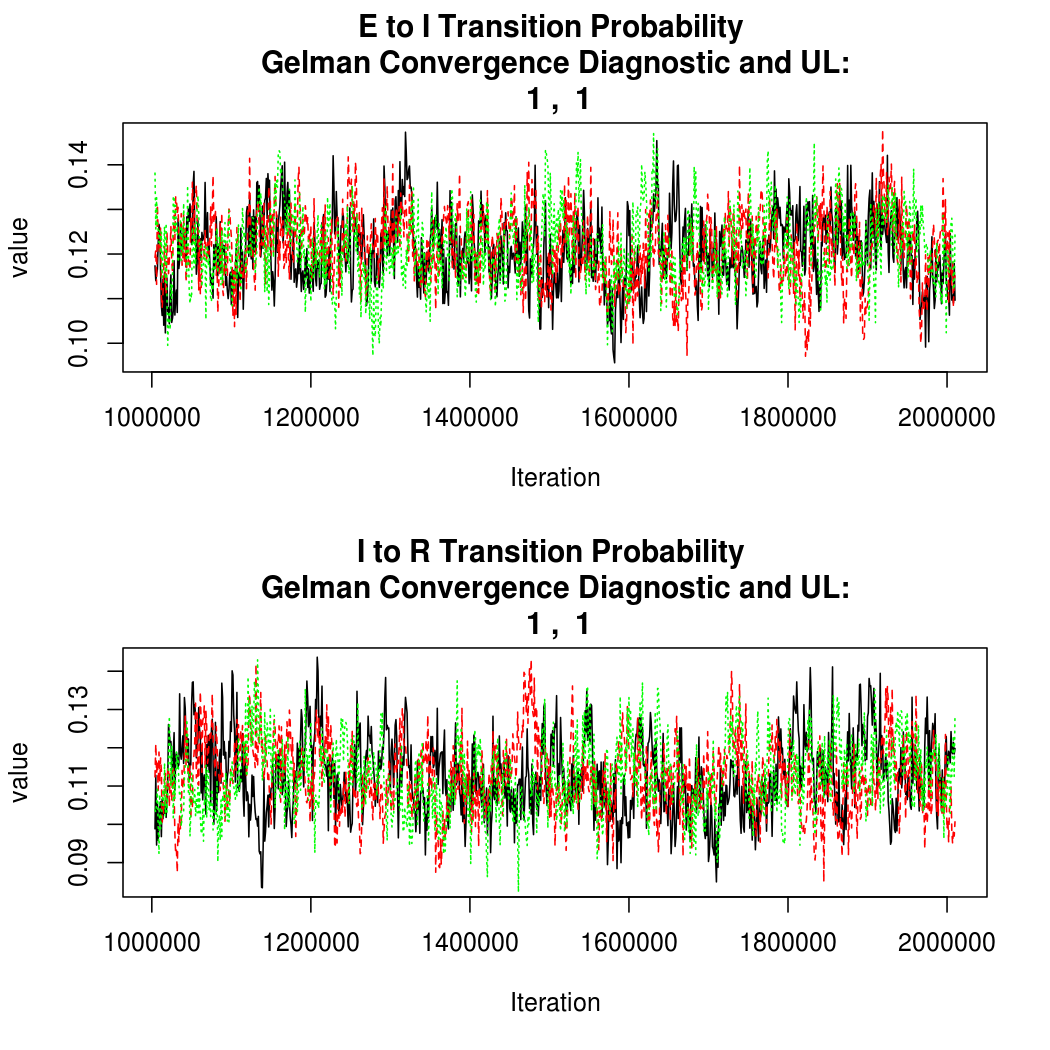
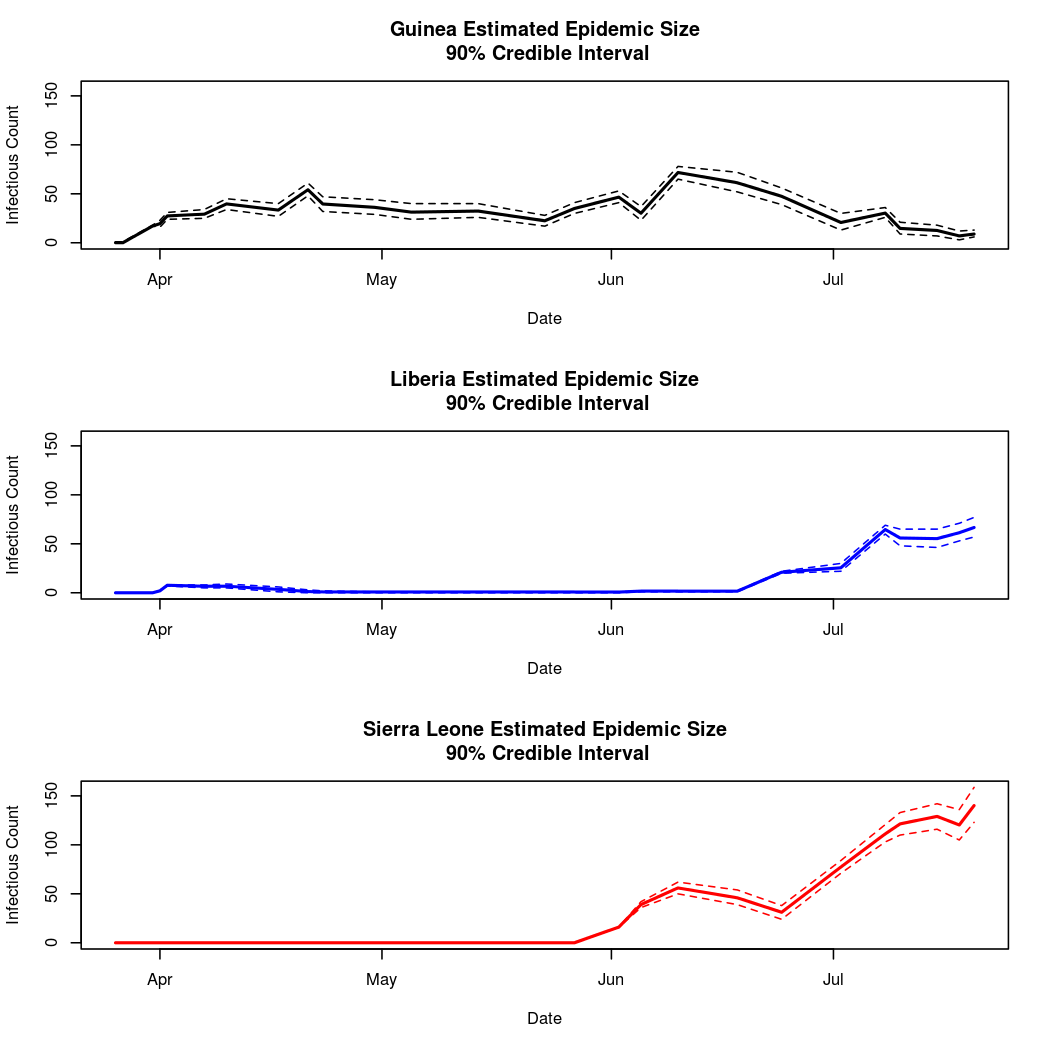
Estimated Epidemic Behavior
The convergence looks reasonable, so let's dissect the estimates a bit.
## Output from coda library summary: ## ########################
## ## Iterations = 1:1007 ## Thinning interval = 1 ## Number of chains = 3 ## Sample size per chain = 1007 ## ## 1. Empirical mean and standard deviation for each variable, ## plus standard error of the mean: ## ## Mean SD Naive SE Time-series SE ## Guinea Intercept -4.560 0.24577 0.004471 0.010948 ## Liberia Intercept -2.649 0.21626 0.003935 0.008239 ## Sierra Leone Intercept -3.291 0.21931 0.003990 0.008992 ## Linear Time Component 7.364 1.21508 0.022107 0.052472 ## Quadratic Time Component -8.474 0.82822 0.015068 0.036330 ## Cubic Time Component 2.700 0.53675 0.009766 0.030400 ## Spatial Dependence Parameter 0.216 0.03330 0.000606 0.001096 ## E to I probability 0.121 0.00796 0.000145 0.000418 ## I to R probability 0.112 0.00950 0.000173 0.000576 ## ## 2. Quantiles for each variable: ## ## 2.5% 25% 50% 75% 97.5% ## Guinea Intercept -5.046 -4.721 -4.559 -4.399 -4.075 ## Liberia Intercept -3.077 -2.791 -2.649 -2.511 -2.225 ## Sierra Leone Intercept -3.725 -3.435 -3.287 -3.141 -2.876 ## Linear Time Component 5.018 6.534 7.331 8.168 9.788 ## Quadratic Time Component -10.121 -9.016 -8.460 -7.896 -6.902 ## Cubic Time Component 1.666 2.341 2.699 3.058 3.769 ## Spatial Dependence Parameter 0.158 0.193 0.214 0.237 0.290 ## E to I probability 0.106 0.116 0.121 0.127 0.137 ## I to R probability 0.095 0.106 0.112 0.118 0.133
The average time spent in a particular disease compartment is just one divided by the probability of
a transition between compartments. The units here are days, so we can see that the average infectious time is estimated to be
(roughly) between 7 and 11 days, while the average latent time is (roughly) between 7 and 10 days. In reality, there is a lot
of variability in these times for Ebola, but these seem like reasonable estimates for the average values.
We also notice that there is reasonably strong spatial dependence (the distribution of the spatial dependence parameter is well separated from zero), indicating reasonably strong mixing between the three populations. This is unsurprising, as the disease has in fact spread between all three nations.
It also appears that Guinea has the lowest estimated epidemic intensity, followed by Sierra Leone and Liberia, which have similar credible
intervals for their intercept parameters.
Basic Reproductive Number Calculation
A common tool for describing the development and containment of an epidemic is a quantity known as the basic reproductive numer, or the basic reproductive ratio, or one of several other variants on that theme. The basic idea is to quantify how many secondary infections an infected individual is expected to cause in a large, fully susceptible population. Naturally, when this ratio exceeds one we expect it to spread. Conversely, a basic reproductive number less than one indicates that a pathogen is more likely to die out. This software library doesn't yet compute the ratio automatically, but does provide what's known as the "next generation matrix" which can be used to quickly calculate the quantity.
In addition to coming up with a point estimate of the ratio, it is helpful to quantify the uncertainty in the estimates obtained. Unfortunately, we can't just grab this from the MCMC output so far. Fortunately, we can just perform more samples and compute the ratio along the way as shown in the code below.
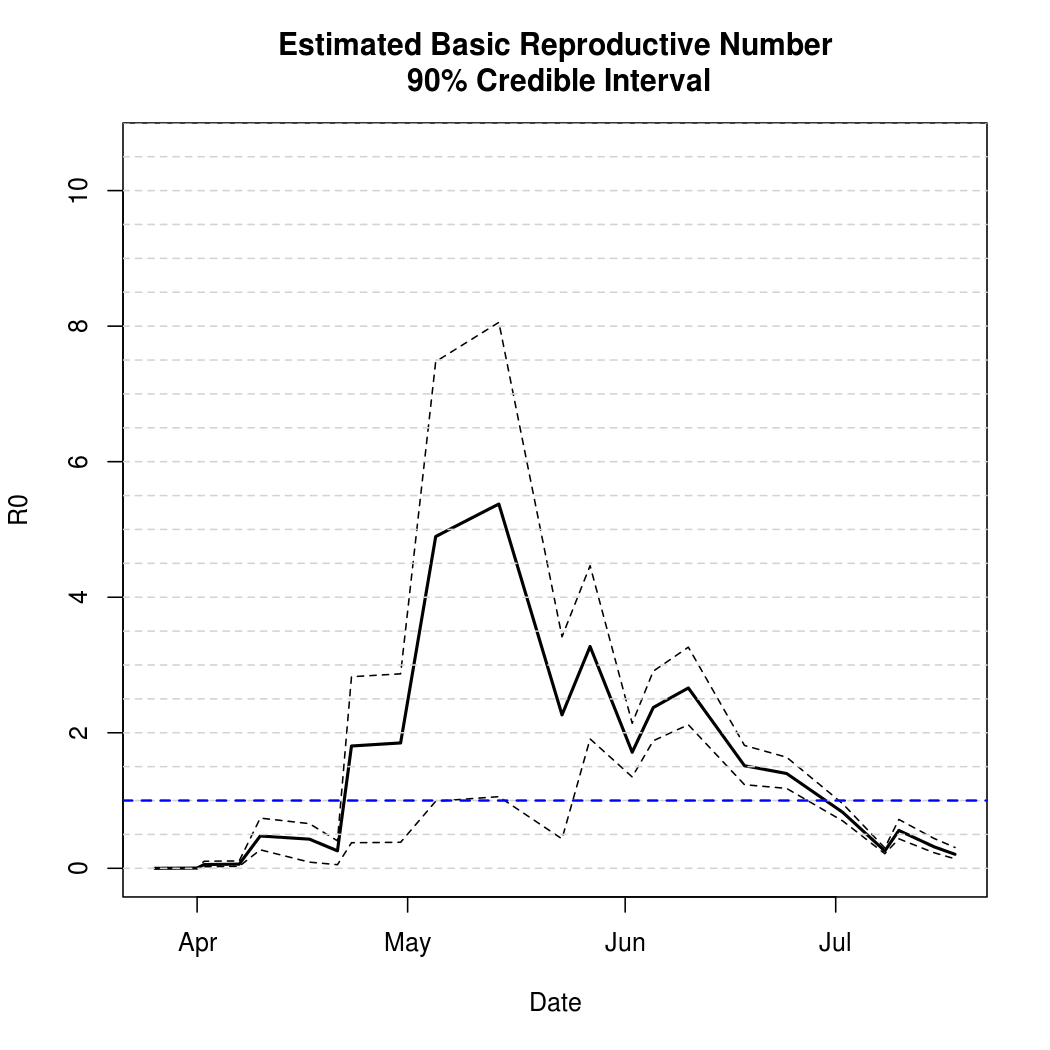
While the basic reproductive number is a useful quantity to know, it does not directly make any predictions about future epidemic behavior. In order to do that, we need to simulate epidemics based on the MCMC samples we have obtained and summarize their variability over time.
Epidemic Prediction
Currently the simulation required for epidemic prediction must be done "manually", or by writing a bunch of R code (given below). As the library develops, a simpler prediction interface is a high priority.
Below, we will attempt to predict the course of the epidemic through early fall.
We must be cautious when making predictions about a chaotic process this far into the future. We must be particularly cautious becase the basis chosen for the temporal trend in the epidemic intensity process was polynomial. While polynomial bases often provide a good fit to the data, they can behave unreasonably outside the range over which the model was fit (quadratic and cubic terms can get large very quickly). Analysis 2 will consider, in abbreviated fashion, the results of using a natural spline basis for this process instead. Spline bases extrapolate linearly, and so are less prone to extreme extrapolation errors.
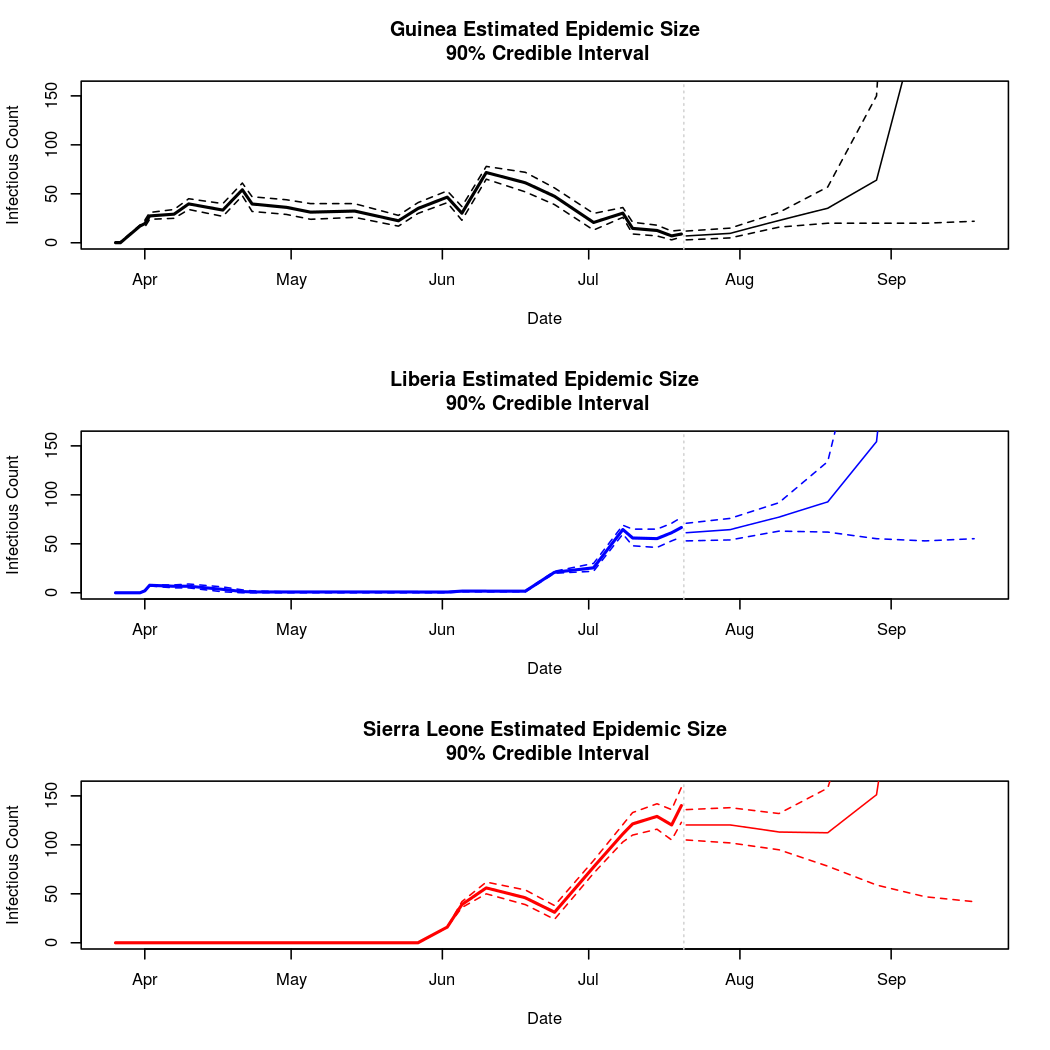
It looks like our worries about polynomial basis functions were well founded. While these predictions are likely acceptable for several days or weeks after the currently available data, they clearly become dominated by higher order polynomial terms as time goes on. There is no data to support these large swings in epidemic behavior, so we can be fairly certain that these long term predictions are extrapolation errors.
On the other hand,
Analysis 2: Spline Basis
Below is an abbreviated and concatenated modification of the code presented above. We won't be concerned with interpreting the model parameters, as the polynomial model was likely sufficient in terms of estimation.

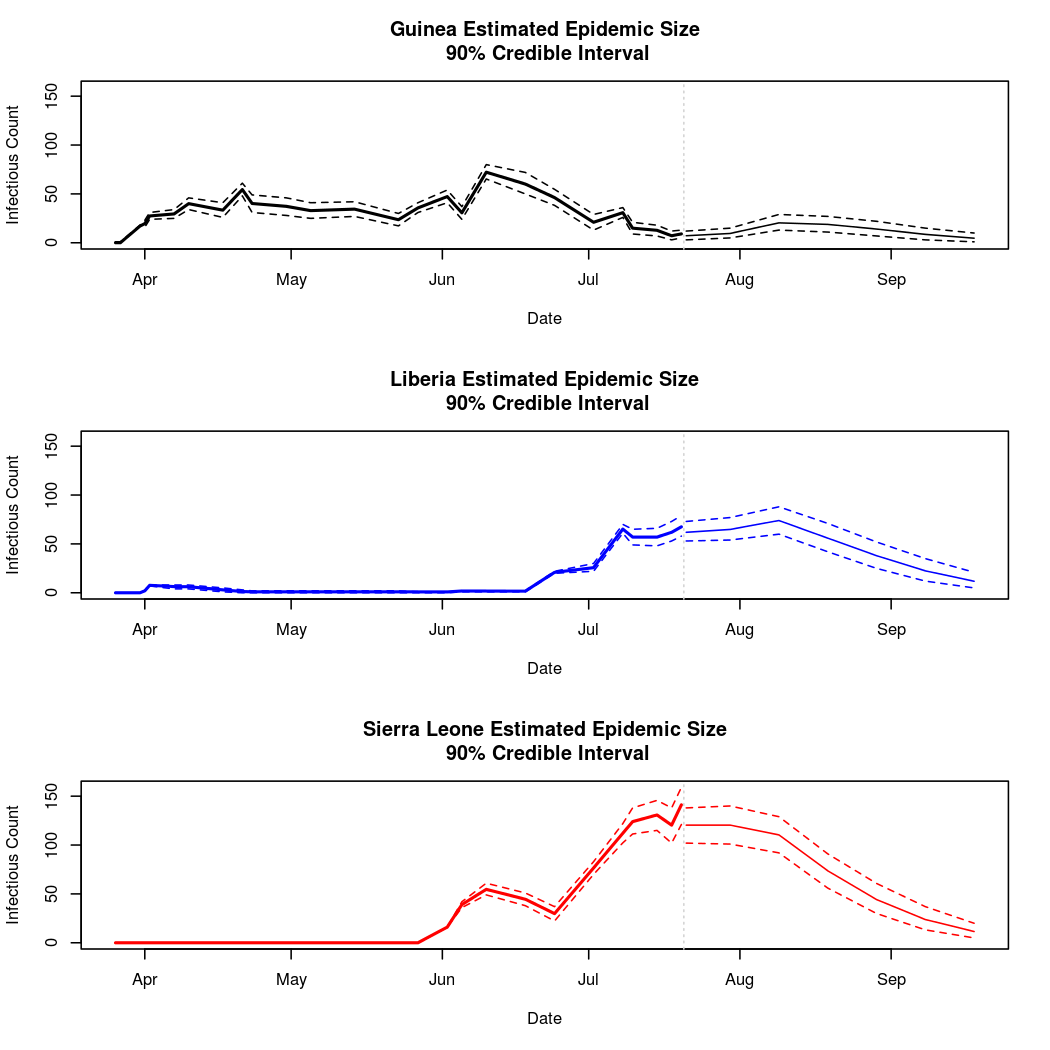
These predictions do appear more reasonable. As the two sets of basis functions give similar answers in the near future, it seems likely that the epidemic will continue at a steady rate for at least the next few weeks, though we must still be careful projecting too far into the future. Still, if I had to bet, I'd bet on a steadily decreasing infection rate dropping towards zero in mid September.
That wraps up the analyses for now, though of course there are numerous other hypotheses we could explore:
- Use time varying co-variates to track the effect of various public health interventions.
- Explore other types of spline bases, as well as bases of different complexity (quartic etc.).
- Obtain better information about population flows between the three countries, or obtain more finely geocoded data to examine the effect on the sub-regional level.